| 摩登7机器人 |
| CHUANGZE ROBOT |
3.1 参数校准方法思路
参考《差速驱动机器人轮间距校准》的思路:控制机器人做自旋运动,运动到目标位姿后停止,观察机器人实际停止位姿与理论停止位姿的偏差,调整构型参数,以尽可能缩小偏差。
为什么可以采用上述自旋方式来校准上述两种全向移动平台的构型参数?
观察公式(3-4),当全向机器人仅做自旋运动时的运动学方程,所有驱动轮的转速大小相同,在轮直径已校准的前提下,所有驱动轮按照设定大小的转速朝设定的方向转动,那么机器人将会以确定的角速度绕几何中心旋转,如果机器人几何中心角速度是准确的,则运动设定时间后,机器人会停留在确定的位姿(是可通过运动学方程计算的),假如停留的实际位姿和理论计算位姿不重合,则说明公式(3-4)中的参数不准确,也就是机器人构型参数不准确,故需要调整构型参数,以实现上述停留的实际位姿和理论计算位姿尽可能重合,当位姿重合时对应的构型参数就是实际准确的参数,也就校准完成了。
3.2 全向轮移动平台参数校准
基于上述分析,这里先以全向轮移动平台为例,结合理论推导,阐述校准过程。
同样的,为便于观察自旋运动停止后的位姿,所以设定机器人匀速自旋整周,这样便于对比自旋整周前后的位姿偏差,自旋整周所需时间t可表示为
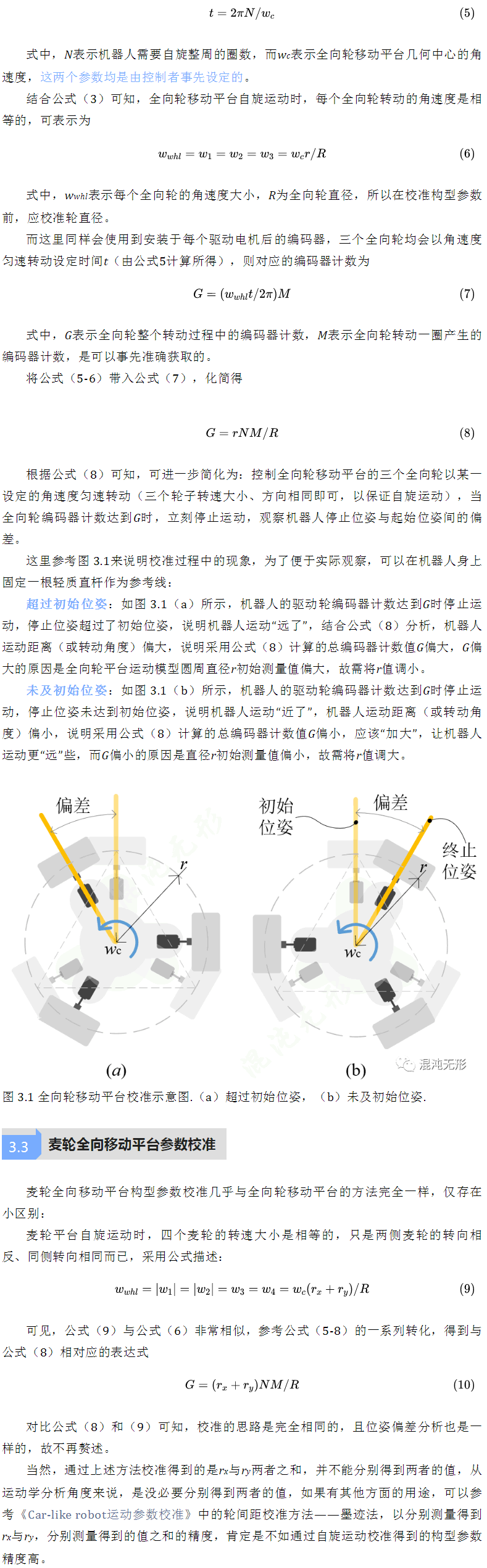
通过前文的论证分析,可以看出全向移动平台的构型参数校准原理和方法都非常相似,但是也存在一定差异:在《常见移动机器人多角度对比分析》一文中有提到,全向移动机器人的质量分布对机器人运动精度是存在较大影响的,质量分布不均,即使控制机器人驱动轮转速相同,也难以实现出色的自旋运动,且麦轮全向移动平台是4个驱动轮,准确控制难度是比全向轮全向平台要大的,运动控制更有难度。
而从前文分析可知,正确的校准流程是:先调节机器人质量分布,保证机器人能够做严格的直线运动和自旋运动,接着再校准驱动轮的轮直径《常见移动机器人轮直径校准》,后再校准本文提到的构型参数。
“转自微信公众号:混沌无形”
 |
| 机器人公司 机器人应用 智能医疗 物联网 机器人排名 机器人企业 机器人开发 独角兽 消毒机器人品牌 |